[알고리즘] 위상정렬(그래프 정렬)

(문제) 위상정렬(그래프 정렬)

---

위상정렬은 어떤 일을 하는 순서를 찾는 알고리즘입니다.

각각의 일의 선후관계가 복잡하게 얽혀있을 때 각각 일의 선후관계를 유지하면서 전체 일의 순서를 짜는 알고리즘입니다.

만약 아래와 같은 일의 순서를 각각 지키면서 전체 일의 순서를 정한다면

1 4 //1번일을 하고 난 후 4번일을 해야한다.
5 4
4 3
2 5
2 3
6 2

전체 일의 순서는 1, 6, 2, 5, 4, 3과 같이 정할 수 있다.

전체 일의 순서는 여러 가지가 있습니다 그 중에 하나입니다.

입력설명

첫 번째 줄에 전체 일의 개수 N과 일의 순서 정보의 개수 M이 주어집니다.

두 번째 줄부터 M개의 정보가 주어집니다.

출력설명

전체 일의 순서를 출력합니다.

테스트케이스

입력예제	출력예제
6 6 1 4 5 4 4 3 2 5 2 3 6 2	1 6 2 5 4 3

---

해결방법

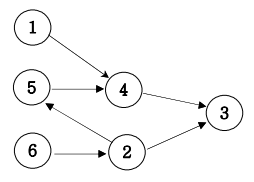
1. 입력을 손으로 그래프로 그려 본다.
2. 진입 차수를 구한다. (차수 : 노드의 각 연결된 선의 개수)
   (진입차수 : 노드의 각 연결된 선 중에서 들어오는 것)
   위의 예 같은 경우, 4는 진입차수가 2개이다 (1, 5)
3. dt라는 인접행렬을 만든다.
4. 이 인접행렬을 입력으로 받은 값 중 2번 째 값이 나타내는 인접형렬의 인덱스를 +1 하여 초기화 한다.
5. 큐를 생성하여 dt에 초기화 한 값들 중 0의 값이 들어있는 인덱스 번호를 append 한다.
6. 큐에서 맨 앞의 값 하나를 꺼낸 후, 그 값을 출력한다.
7. 출력한 값을 갖는 진입차 수들의 값을 -전부 -1 한다. (1은 4의 진입차수 이므로 dt의 4번째 index 값을 -1 한다)
   
8. 다시 큐에서 맨 앞에 값 하나를 꺼낸 후, 그 값을 출력하여 7번과 같은 방법을 이용하여 작동 시킨다.
9. 이렇게 index의 값을 -1 할 때! 만약 index의 값이 0이 될 경우, 그 인덱스 번호를 다시 큐에 append 한다.
10. 이 작업을 모든 degree가 0이 될 때 까지 반복한다.

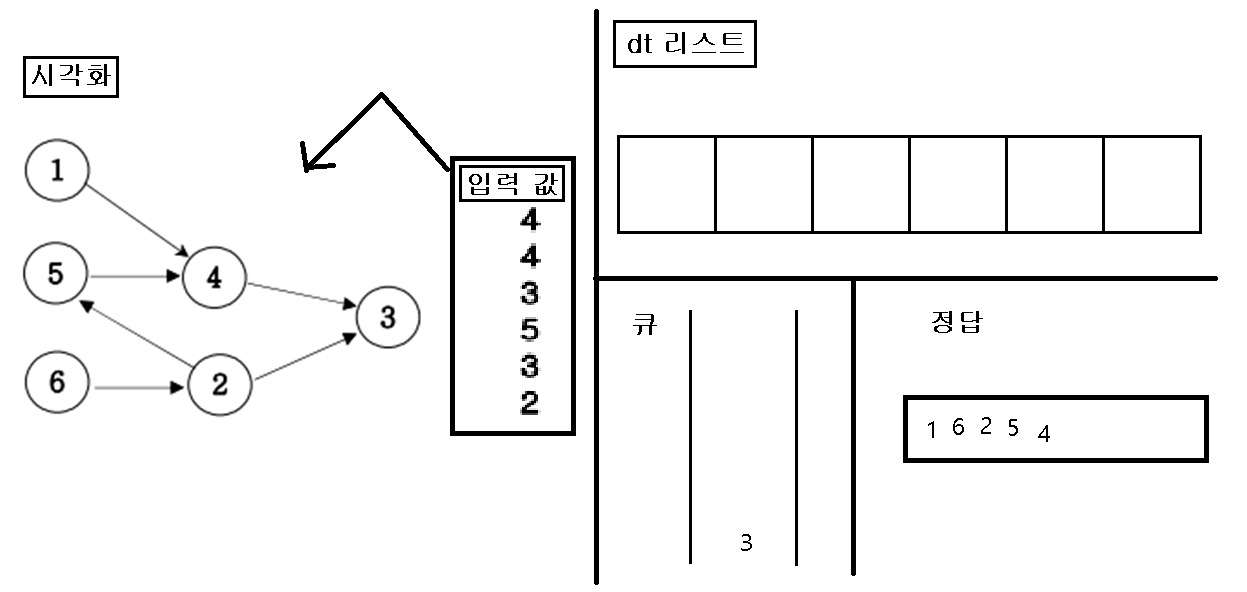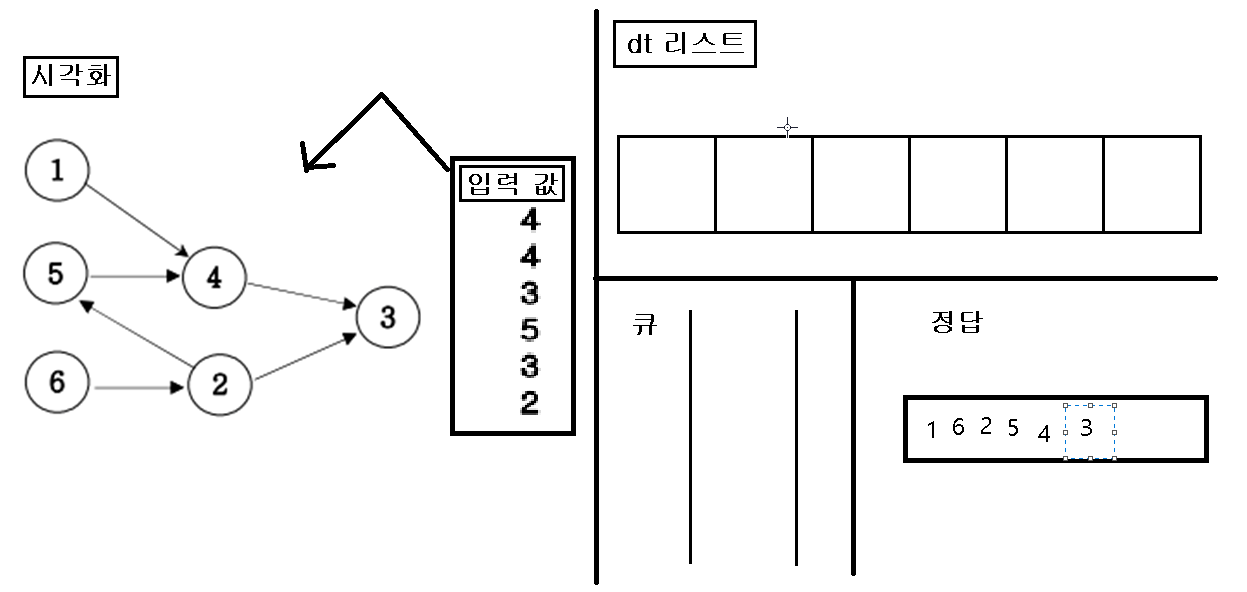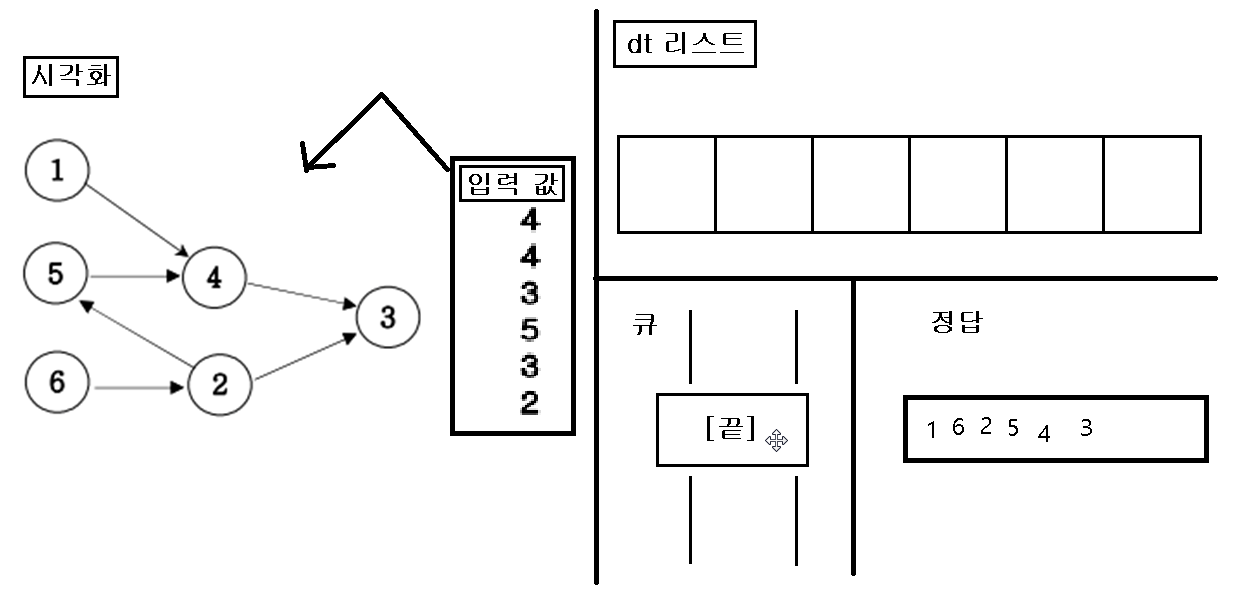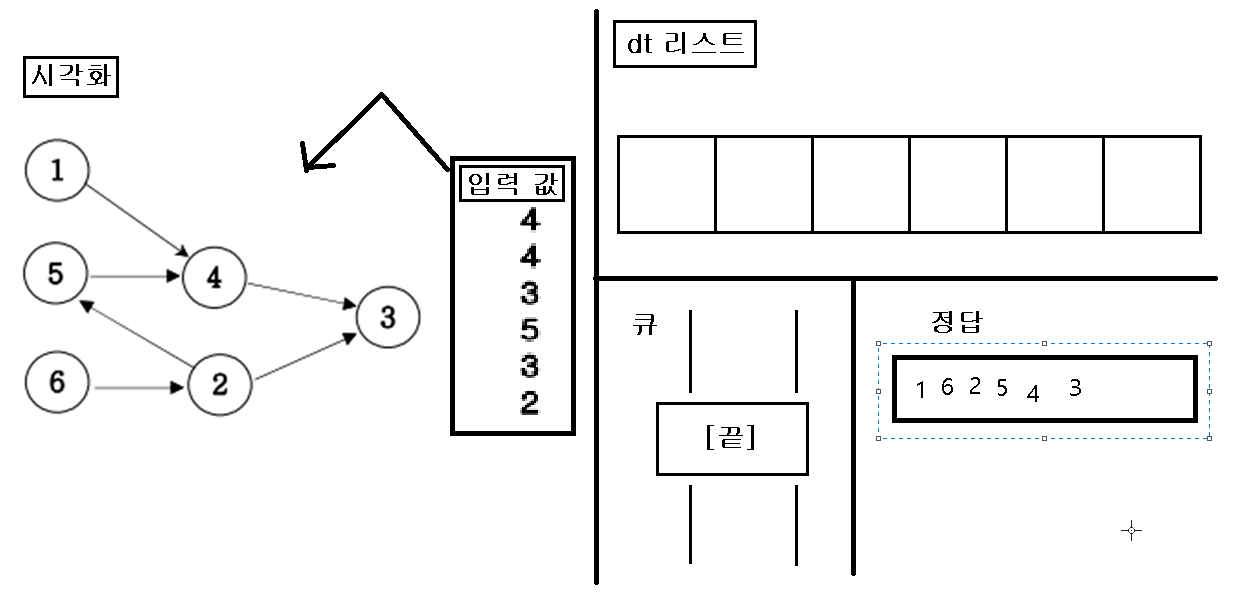
동작 시각화

1. 입력을 가지고 인접행렬을 초기화 한다.

---

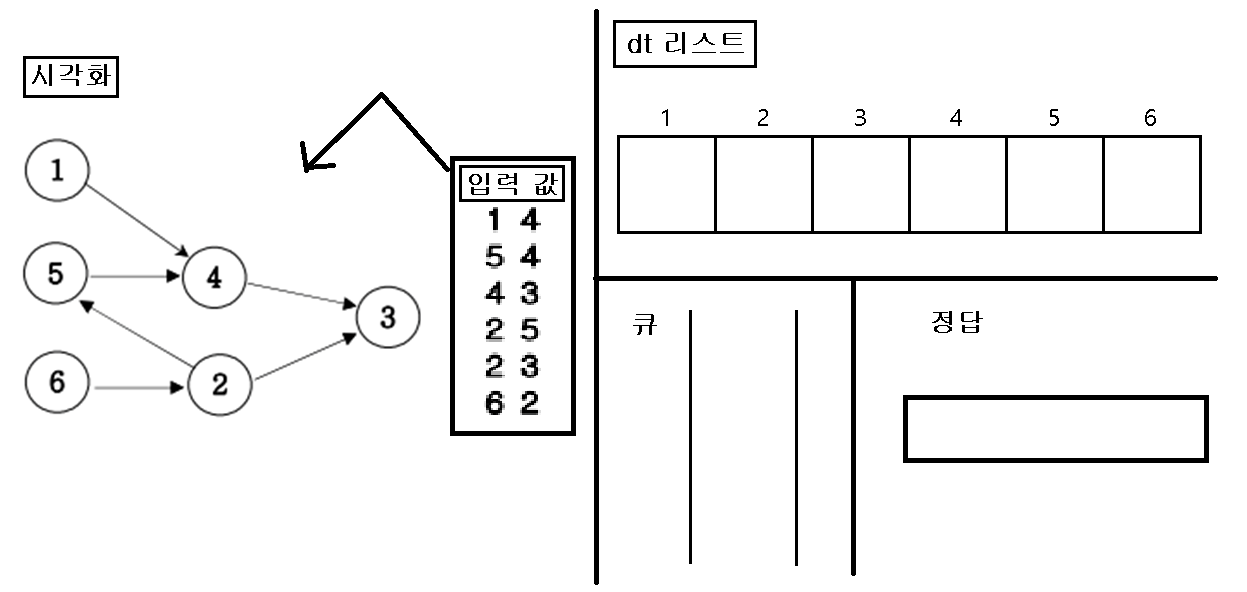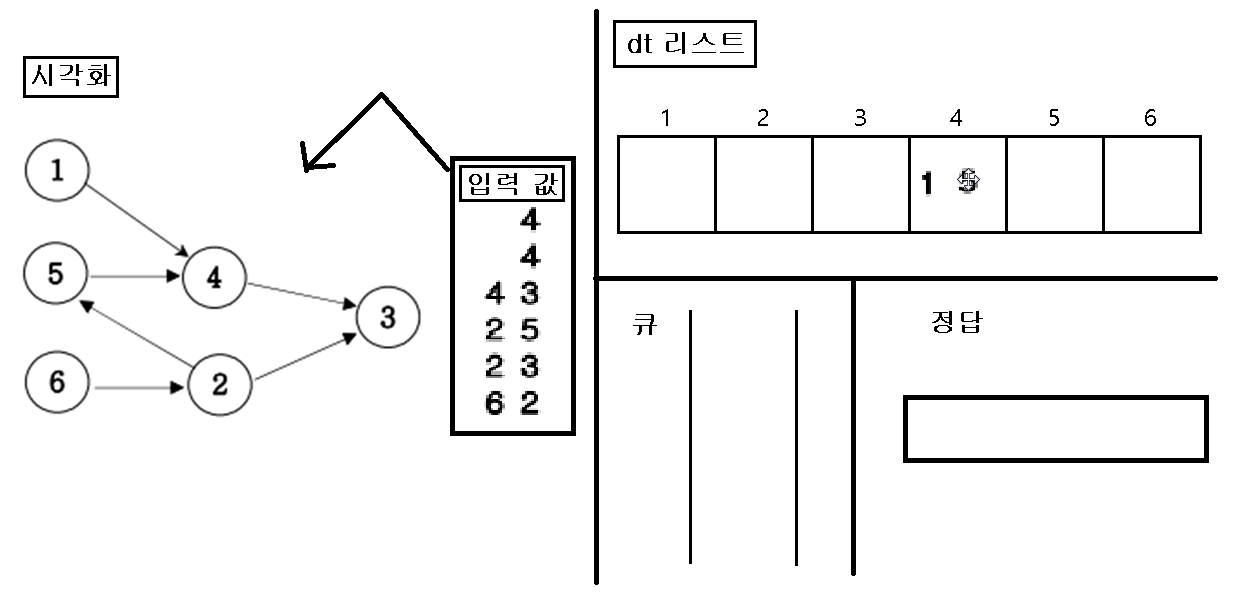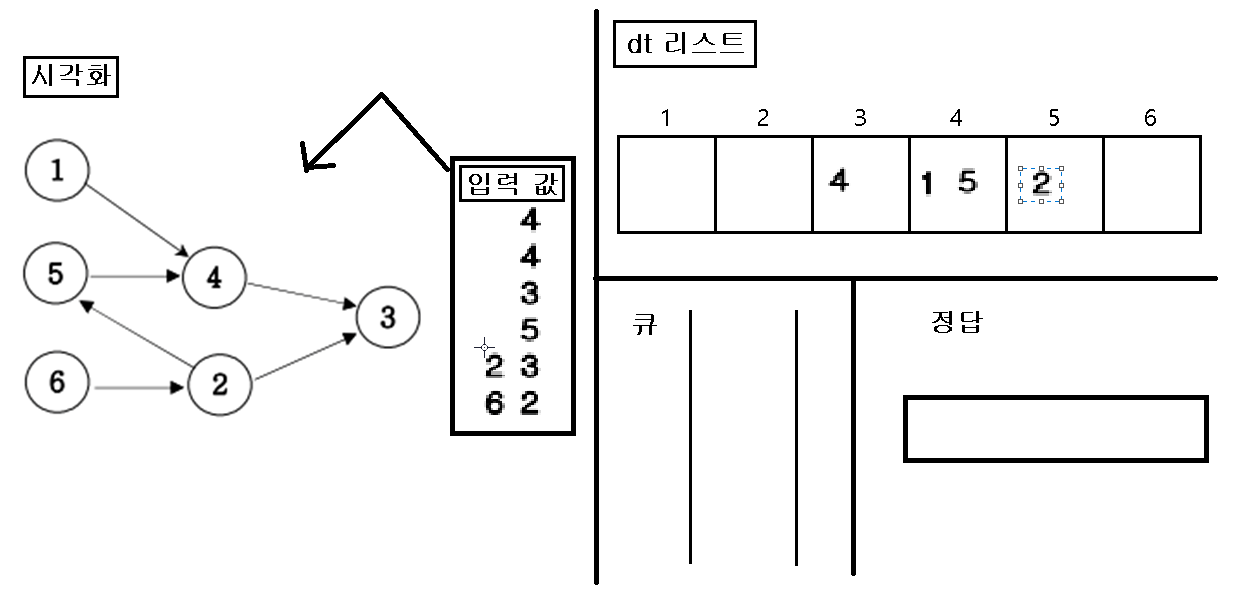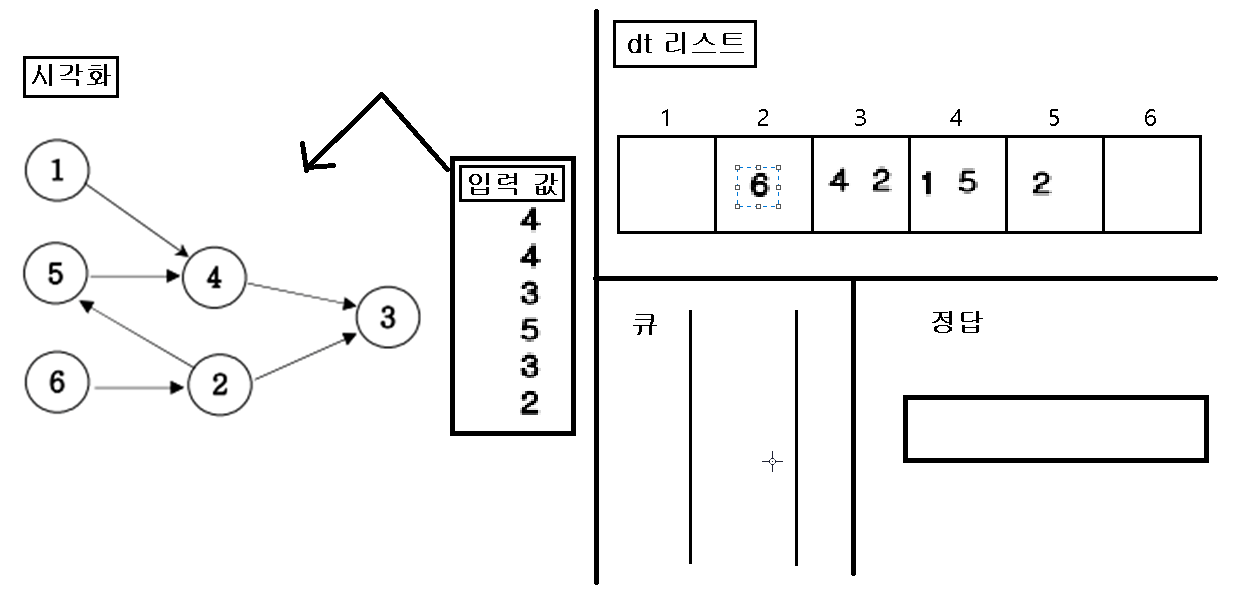
2. 초기화 한 인접행렬에 값이 없는 인덱스 번호를 “큐”에 삽입한다.

---

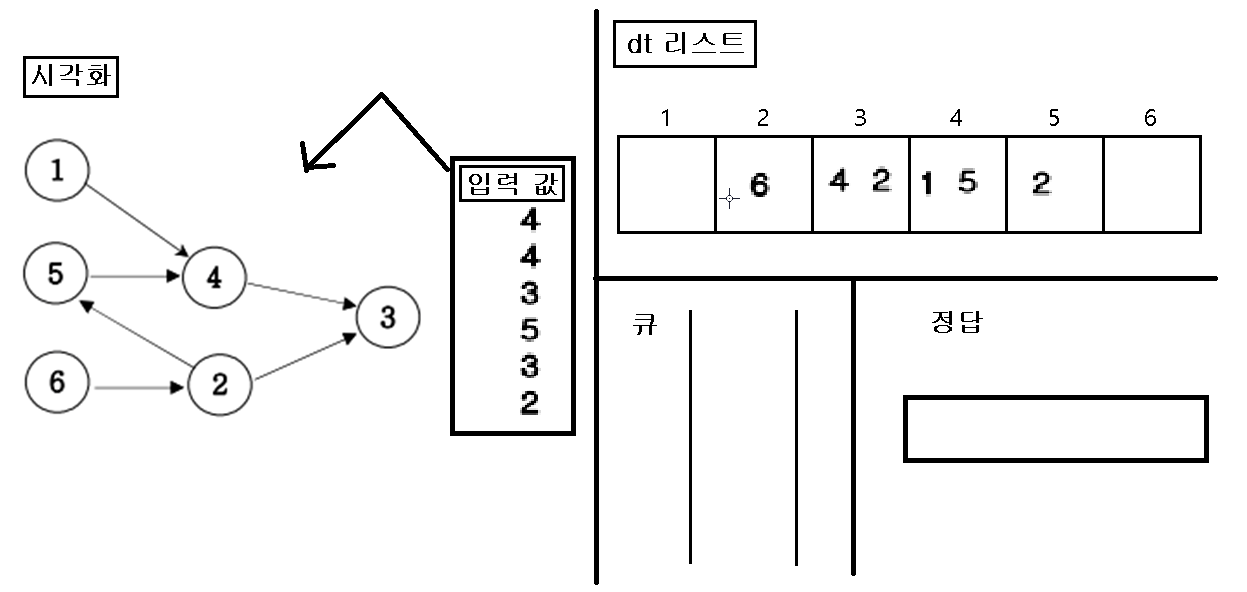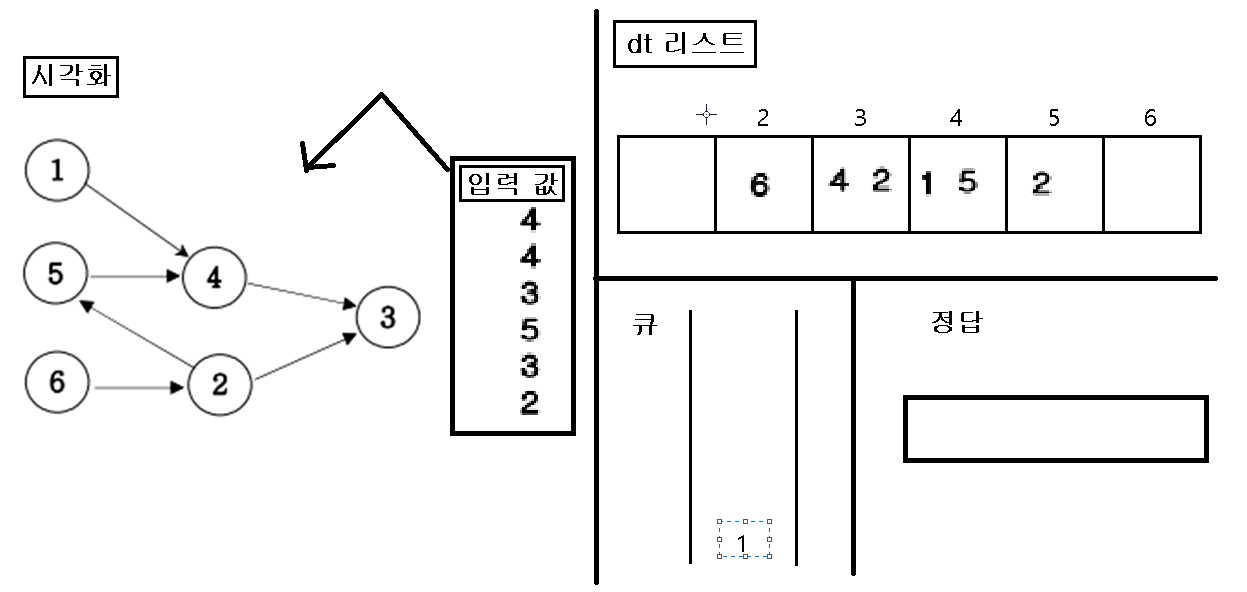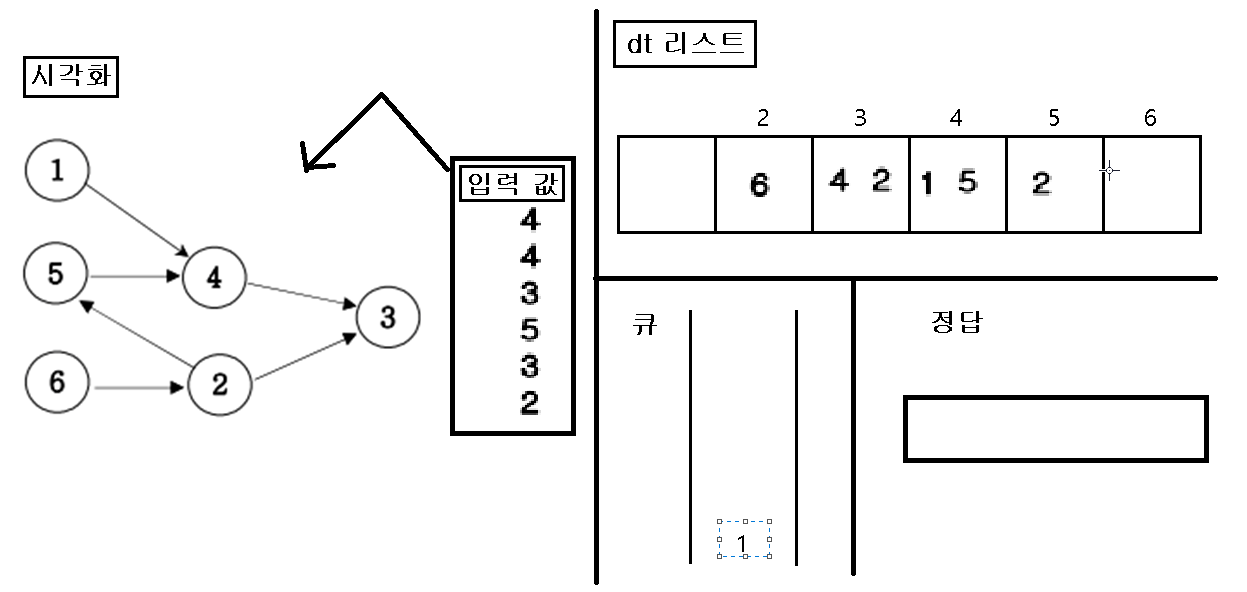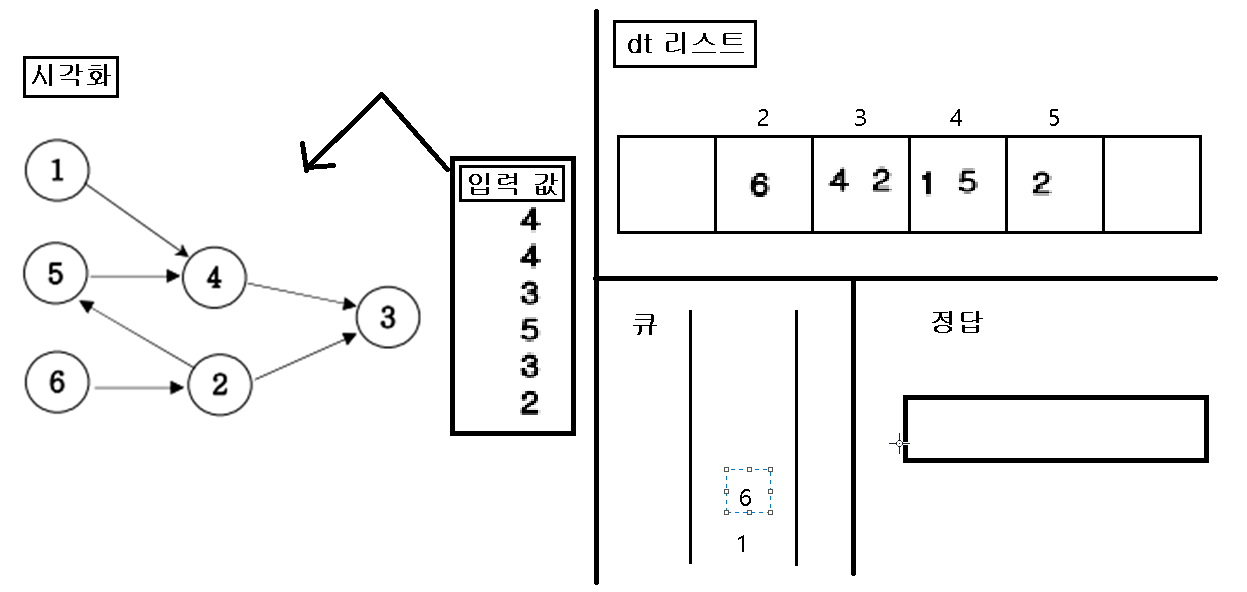
3. “큐”에 삽입한 인덱스 번호를 pop 하여 pop 한 값을 정답 리스트에 삽입하고, pop 된 인덱스 값을 가지고 있은 dt 값을 삭제를 한다.

---

4. dt값을 삭제를 한 후, 만약 값이 비면 비어진 dt 인덱스를 “큐”에 삽입한다.

---

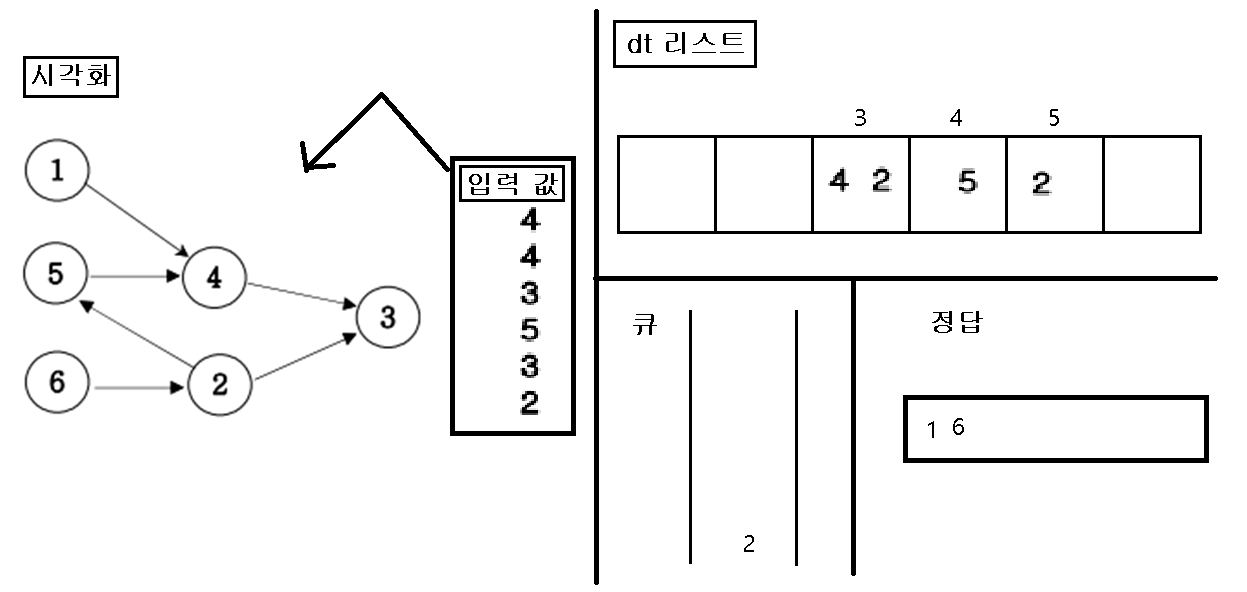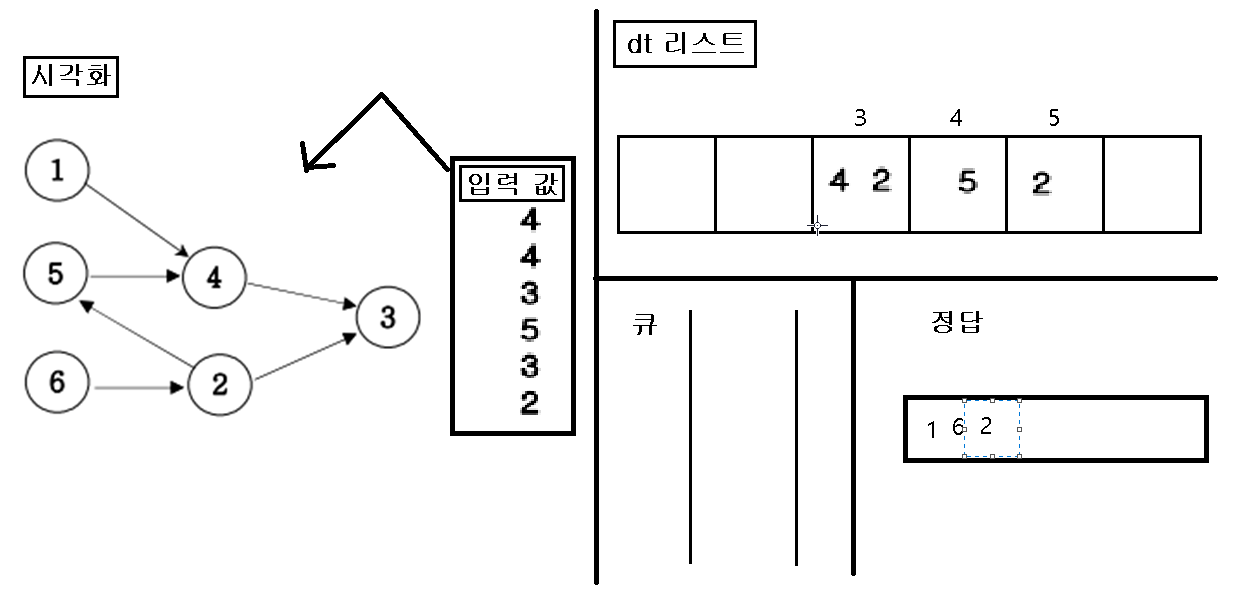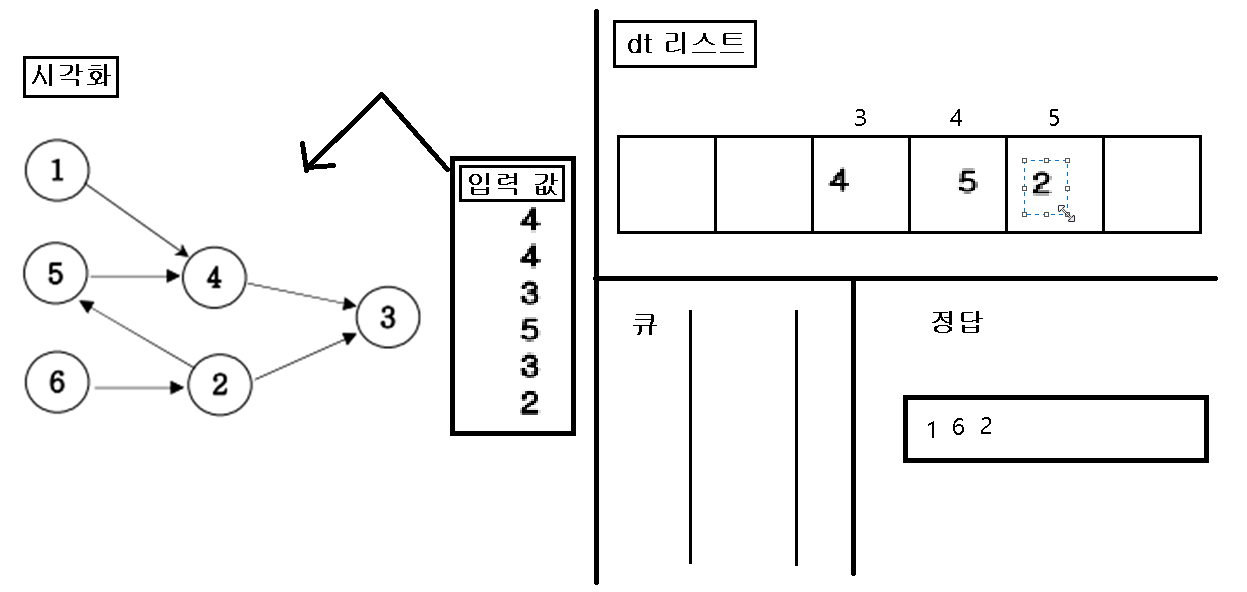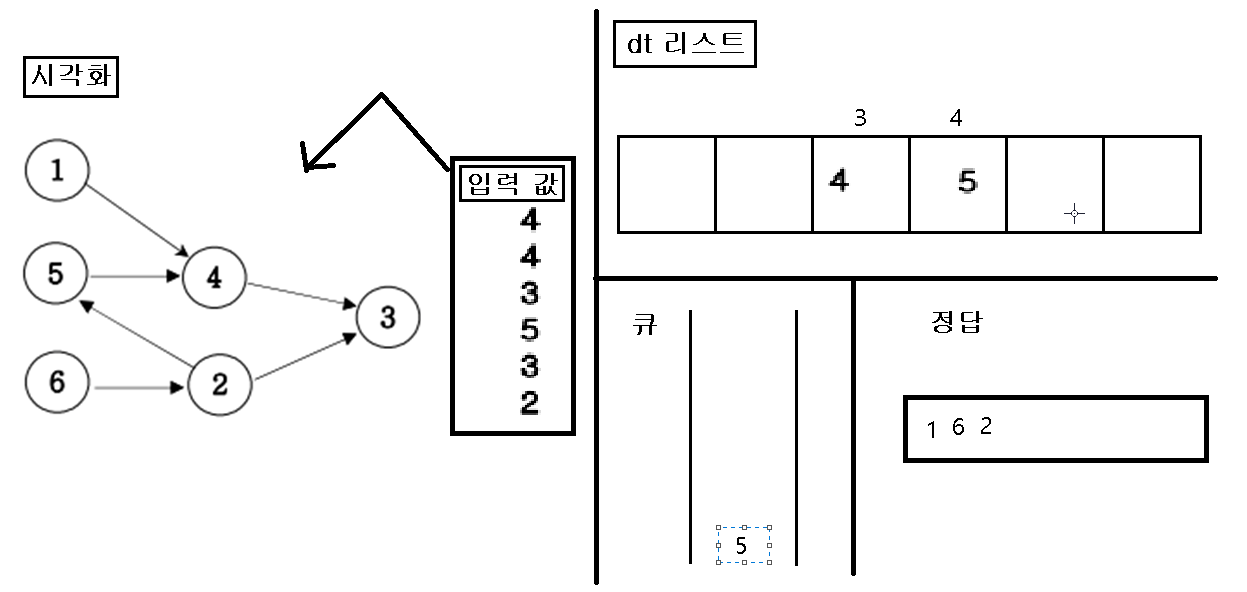
5. 위의 작업을 “큐”에 아무것도 없을 때 까지 반복을 한다.

---

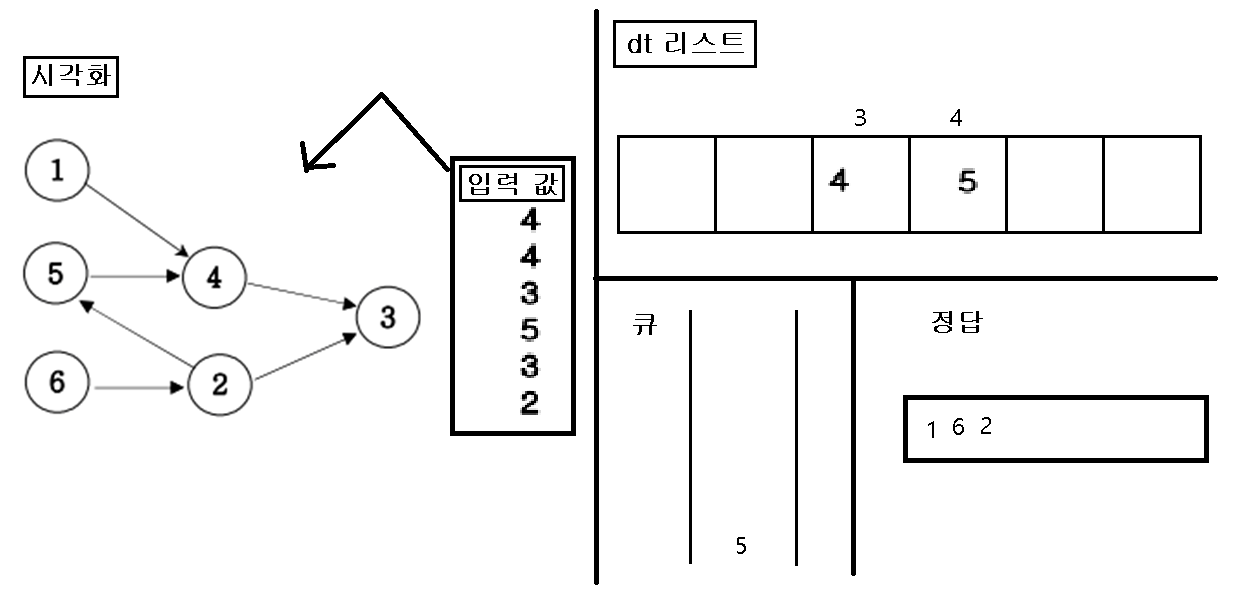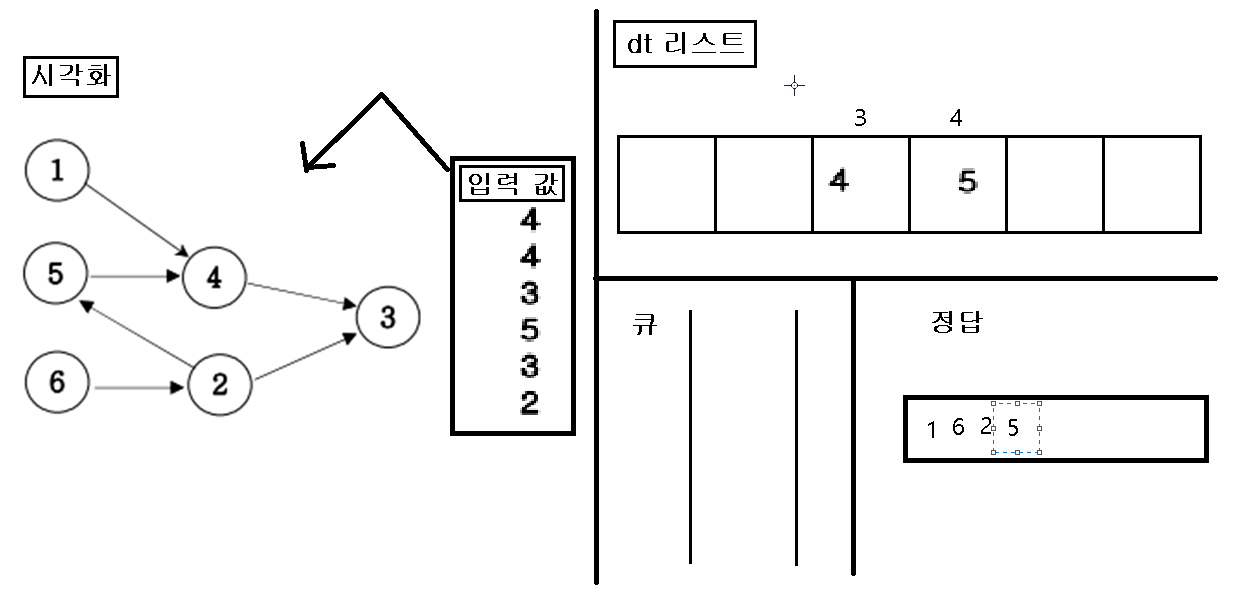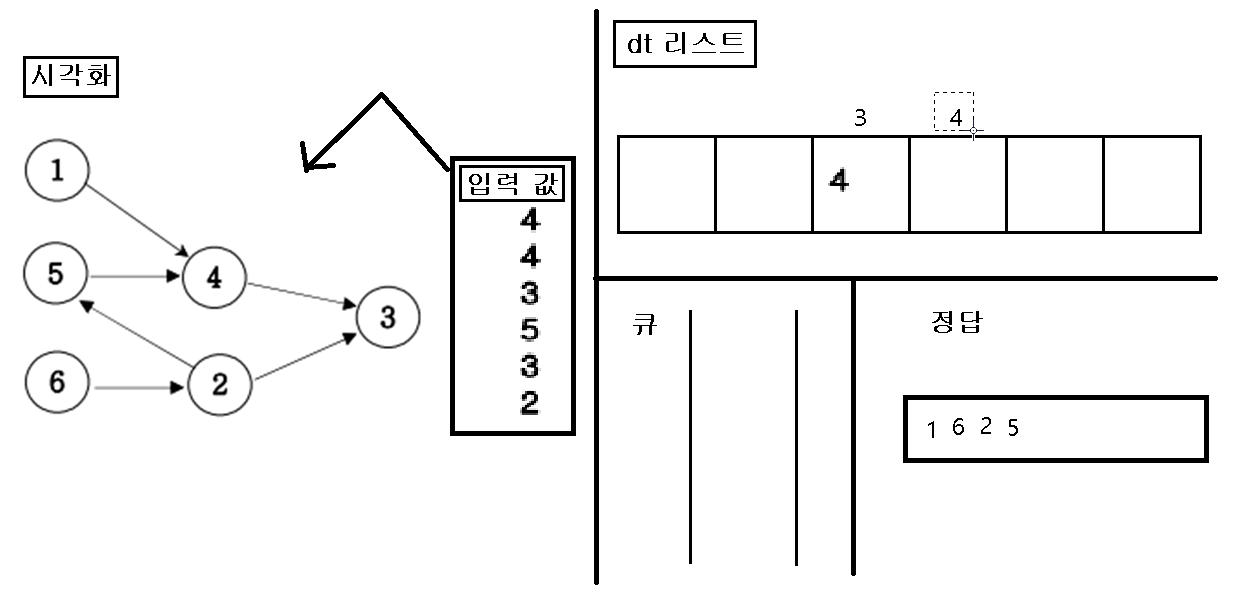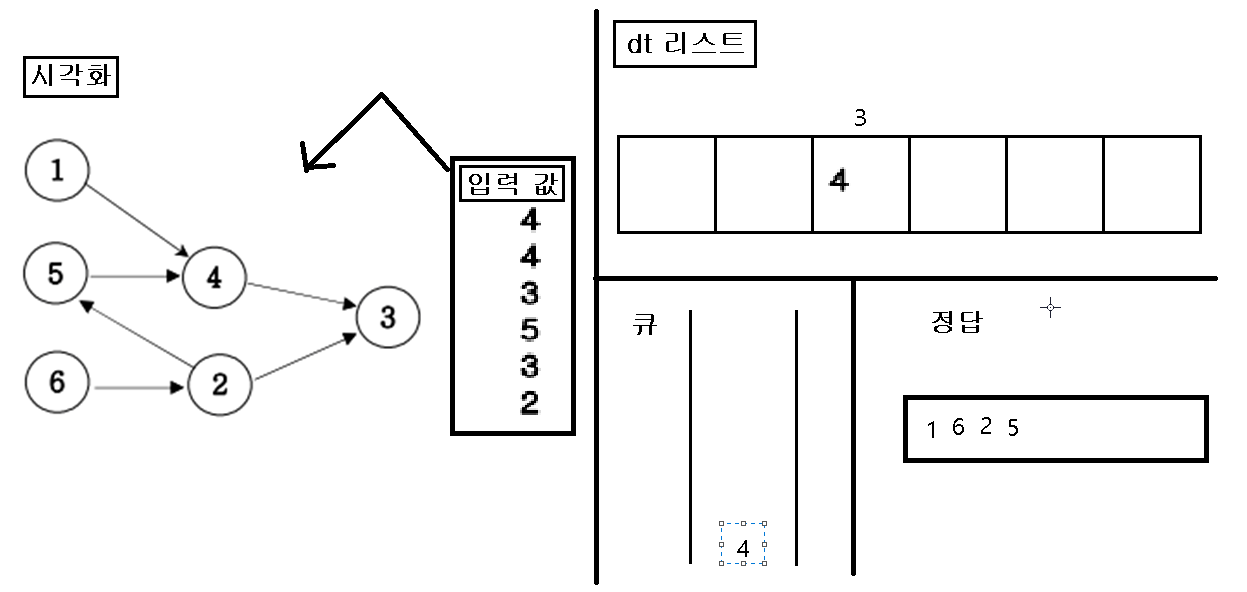
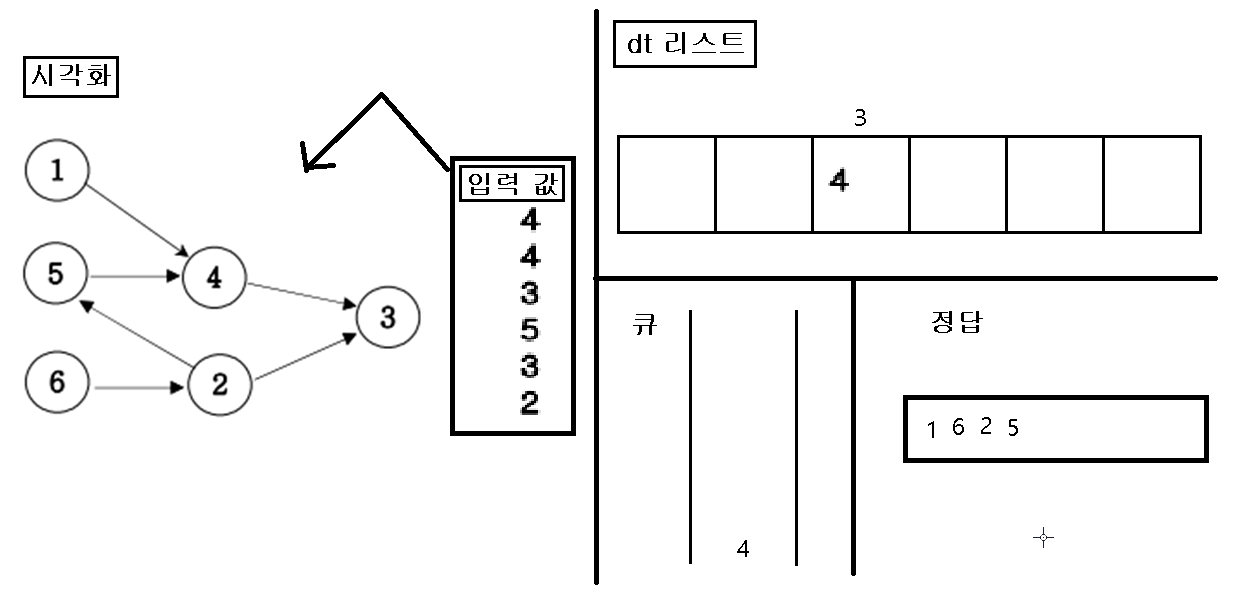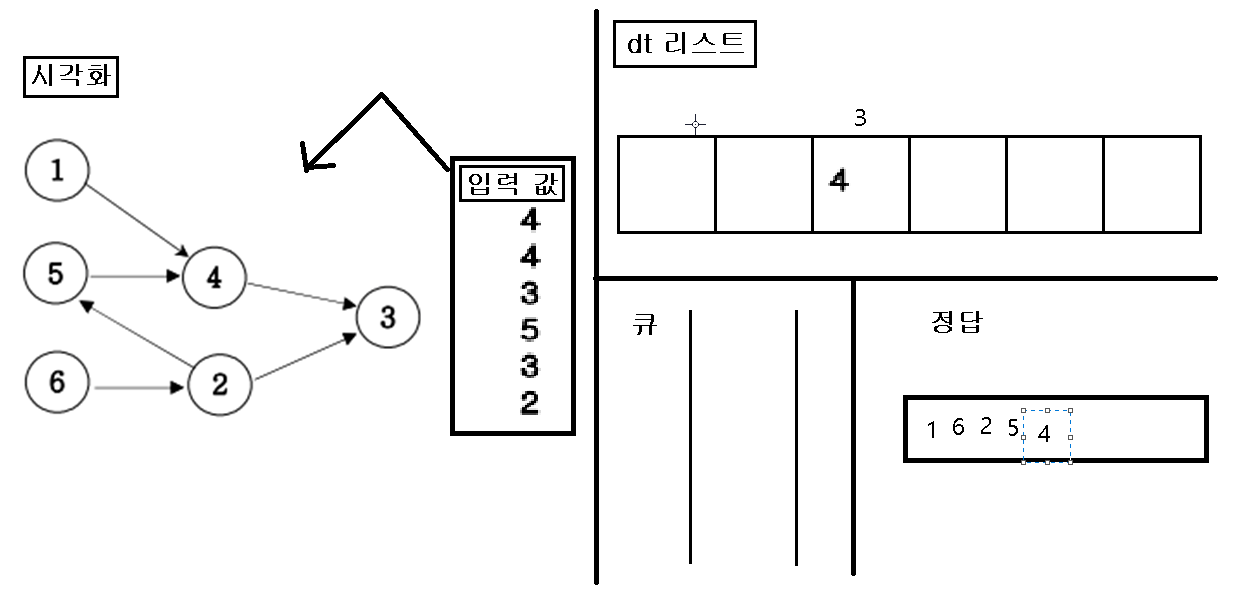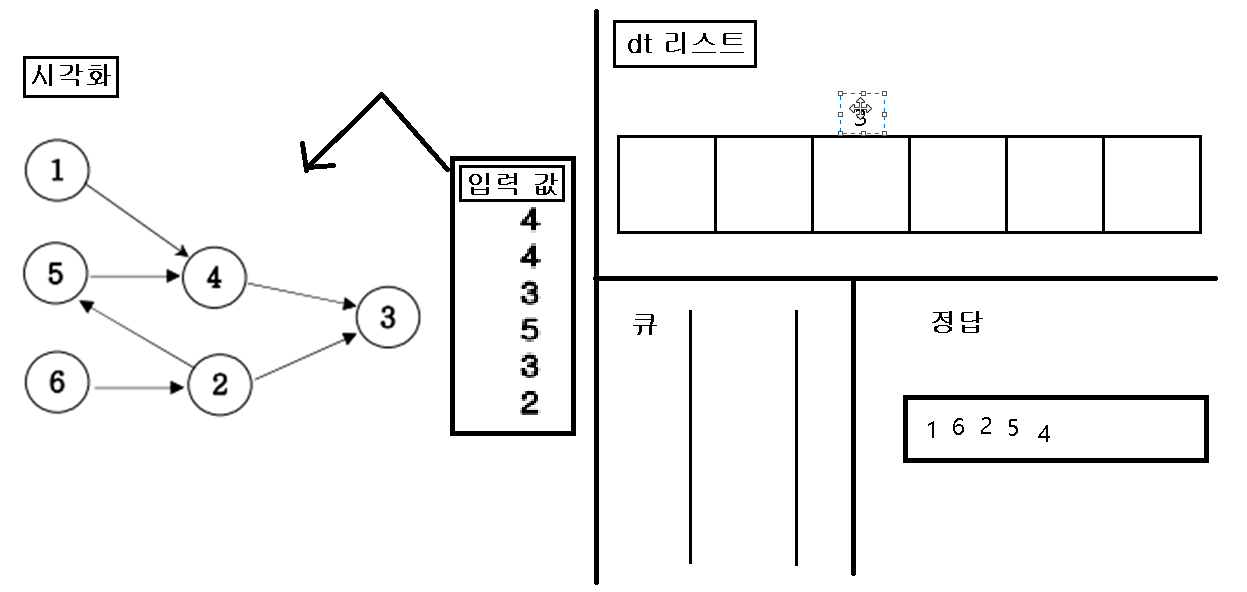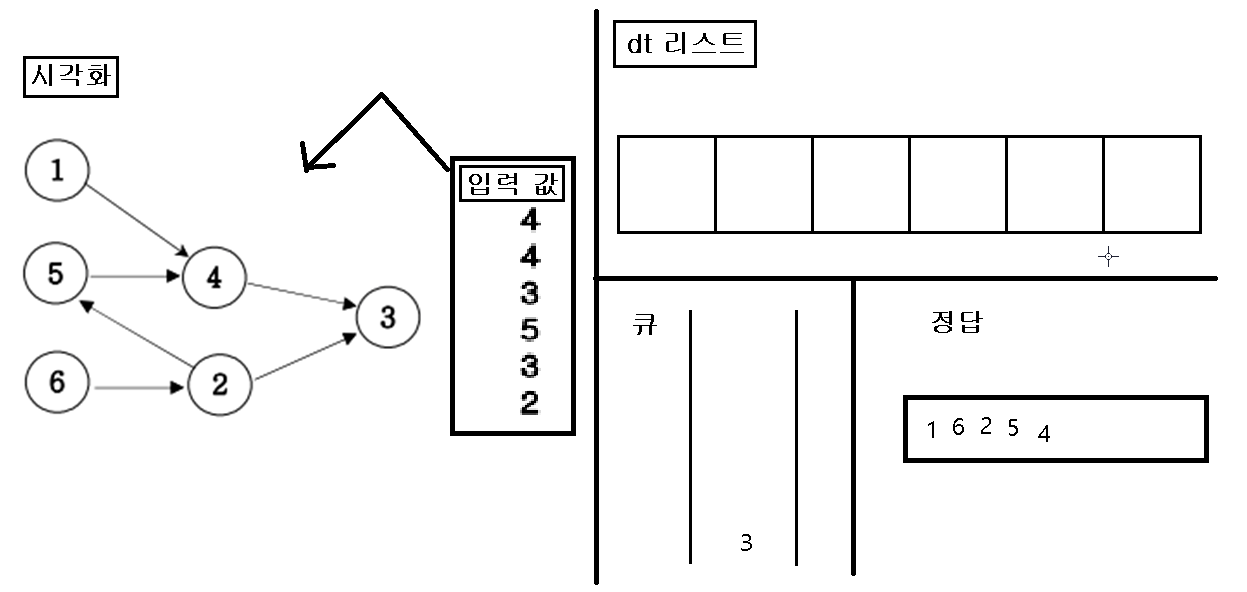
6. 끝나면 정답 리스트를 출력한다.

---

코드

from collections import deque

# n : 일의 개수
# m : 일 끼리의 연결 방법 개수
n, m = map(int, input().split())

# 어떤 인덱스가 진입 차수인지를 기억하기 위해서 2차원 리스트 사용
dt = [[] for _ in range(n)]

# 위상 정렬을 해결하기 위한 자료구조 큐 생성
dQ = deque()

# 정답 저장하는 공간
answer = []

for _ in range(m):
    # s : 시작 노드
    # e : 끝 노드
    # s를 마쳐야 e를 할 수 있음
    s, e = map(int, input().split())
    # 진입차수를 저장 (-1 한 이유는 인덱스를 0에서 시작하기 위해서)
    dt[e-1].append(s-1)

for i in range(n):
    # dt의 값중 아무것도 진입 차수가 없을 경우
    if len(dt[i]) == 0:
        # 큐에 해당 인덱스 정보를 삽입
        dQ.append(i)


while(dQ):
    # 시작한 진입 차수
    st = dQ.popleft()
    # 정답 저장
    answer.append(st+1)
    for i in range(n):
        # 있을 경우 삭제
        if dt[i].count(st):
            dt[i].remove(st)
            # 만약 삭제하고 아무것도 없으면 해당 인덱스 큐에 저장
            if len(dt[i]) == 0:
                dQ.append(i)

print(*answer)